对数函数是一种重要的函数，它与指数函数有密切的关系。在本课时中，我们将学习对数函数的定义、图象和性质，以及如何利用对数函数解决一些实际问题。
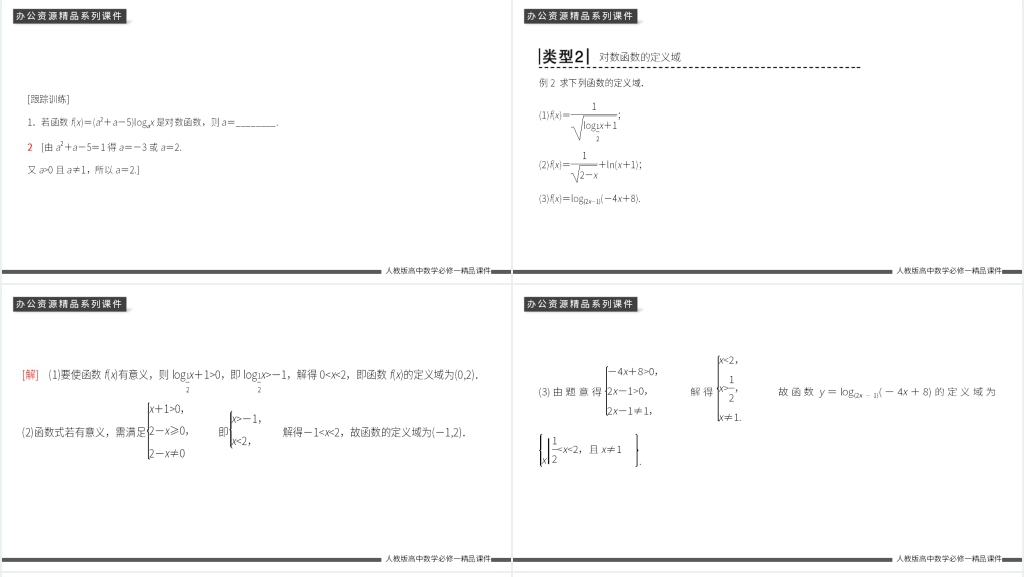
对数函数的定义是：如果a是一个正数且不等于1，那么函数y=log_a x（读作以a为底x的对数）的定义域是(0, +∞)，值域是(-∞, +∞)。这个函数的意义是：如果y=log_a x，那么a^y=x，即y是使得a^y=x成立的唯一实数。
对数函数的图象可以通过指数函数的图象来得到。我们知道，指数函数y=a^x在x轴上方单调递增，且经过点(0, 1)。如果我们把指数函数的图象沿着直线y=x翻折，就可以得到对数函数y=log_a x的图象。对数函数的图象在y轴上方单调递增，且经过点(1, 0)。我们还可以发现，对数函数的图象关于直线y=x对称，即如果点(x, y)在对数函数的图象上，那么点(y, x)也在对数函数的图象上。
对数函数有以下几个基本性质：
- 对任意正数a（a≠1），有log_a 1=0，log_a a=1。
- 对任意正数a（a≠1）和b（b≠1），有log_a b=log_b a。
- 对任意正数a（a≠1）、b和c，有log_a (bc)=log_a b+log_a c。
- 对任意正数a（a≠1）、b和c，有log_a (b/c)=log_a b-log_a c。
- 对任意正数a（a≠1）、b和n（n为整数），有log_a (b^n)=n log_a b。
利用对数函数的性质，我们可以简化一些复杂的算式，或者解决一些实际问题。例如：
- 如果要求2^x=8，我们可以两边取以2为底的对数，得到x=log_2 8=3。
- 如果要求10^(2x-1)=1000，我们可以两边取以10为底的对数，得到2x-1=log_10 1000=3，从而得到x=2。
- 如果要求1000^(3x+2)=10^(6x-4)，我们可以两边取以10为底的对数，得到(3x+2) log_10 1000=(6x-4) log_10 10，由于log_10 1000=3，log_10 10=1，所以得到9x+6=6x-4，从而得到x=-2/3。
这套高一上册《对数函数的图象及性质》第一课时PPT课件属于内容型，已包含实质内容，可直接使用！

超人办公网是一家办公文档资源站，PPT文档资源均来自用户分享，如果损害了你的权利，请联系邮箱我们处理